+inf.0(/ 1.0 -0.0)
-inf.0(/ 0.0 0.0)
+nan.0(/ +inf.0 -inf.0)
+nan.0
This chapter describes Chez Scheme extensions to the standard set of operations on numbers. See Chapter 6 of The Scheme Programming Language, 4th Edition or the Revised6 Report on Scheme for a description of standard operations on numbers.
Chez Scheme supports the full set of Scheme numeric datatypes, including exact and inexact integer, rational, real, and complex numbers. A variety of representations are used to support these datatypes:
Most numbers can be represented in only one way; however, real numbers are sometimes represented as inexact complex numbers with imaginary component equal to zero.
Chez Scheme extends the syntax of numbers with arbitrary radixes from two through 36, nondecimal floating-point and scientific notation, and printed representations for IEEE infinities and NANs. (NAN stands for "not-a-number.")
Arbitrary radixes are specified with the prefix #nr, where n ranges from 2 through 36. Digits beyond 9 are specified with the letters (in either upper or lower case) a through z. For example, #2r101 is 510, and #36rZ is 3510.
For higher radixes, an ambiguity arises between the interpretation of certain letters, e.g., e, as digits or exponent specifiers; in such cases, the letter is assumed to be a digit. For example, the e in #x3.2e5 is interpreted as a digit, not as an exponent marker, whereas in 3.2e5 it is treated as an exponent marker.
IEEE infinities are printed as +inf.0 and -inf.0, while IEEE NANs are printed as +nan.0 or -nan.0. (+nan.0 is used on output for all NANs.)
(/ 1.0 0.0) +inf.0
(/ 1.0 -0.0) -inf.0
(/ 0.0 0.0) +nan.0
(/ +inf.0 -inf.0) +nan.0
The first section of this chapter describes type-specific numeric type predicates. Sections 8.2 through 8.4 describe fast, type-specific numeric operations on fixnums, flonums, and inexact complex numbers (flonums and/or inexact complexnums). The fixnum-specific versions should be used only when the programmer is certain that the operands and results (where appropriate) will be fixnums, i.e., integers in the range (most-negative-fixnum) to (most-positive-fixnum), inclusive. The flonum-specific versions should be used only when the inputs and outputs (where appropriate) are certain to be flonums. The mixed flonum/complexnum versions should be used only when the inputs are certain to be either flonums or inexact complexnums. Section 8.5 describes operations, both arbitrary precision and fixnum-specific, that allow exact integers to be treated as sets or sequences of bits. Random number generation is covered Section 8.6, and miscellaneous numeric operations are covered in the Section 8.7.
The Revised6 Report distinguishes two types of special numeric objects: fixnums and flonums. Chez Scheme additionally distinguishes bignums (exact integers outside of the fixnum range) and ratnums (ratios of exact integers). It also provides a predicate for recognizing cflonums, which are flonums or inexact complex numbers.
procedure: (bignum? obj)
returns: #t if obj is a bignum, otherwise #f
libraries: (chezscheme)
(bignum? 0) #f
(bignum? (most-positive-fixnum)) #f
(bignum? (most-negative-fixnum)) #f
(bignum? (* (most-positive-fixnum) 2)) #t
(bignum? 3/4) #f
(bignum? 'a) #f
procedure: (ratnum? obj)
returns: #t if obj is a ratnum, otherwise #f
libraries: (chezscheme)
(ratnum? 0) #f
(ratnum? (* (most-positive-fixnum) 2)) #f
(ratnum? 3/4) #t
(ratnum? -10/2) #f
(ratnum? -11/2) #t
(ratnum? 'a) #f
procedure: (cflonum? obj)
returns: #t if obj is an inexact complexnum or flonum, otherwise #f
libraries: (chezscheme)
(cflonum? 0) #f
(cflonum? 0.0) #t
(cflonum? 3+4i) #f
(cflonum? 3.0+4i) #t
(cflonum? +i) #f
(cflonum? +1.0i) #t
Fixnum-specific procedures normally check their inputs and outputs (where appropriate), but at optimization level 3 the compiler generates, in most cases, code that does not perform these checks.
procedure: (most-positive-fixnum)
returns: the most positive fixnum supported by the system
procedure: (most-negative-fixnum)
returns: the most negative fixnum supported by the system
libraries: (chezscheme)
These procedures are identical to the Revised6 Report greatest-fixnum and least-fixnum procedures.
procedure: (fx= fixnum1 fixnum2 ...)
procedure: (fx< fixnum1 fixnum2 ...)
procedure: (fx> fixnum1 fixnum2 ...)
procedure: (fx<= fixnum1 fixnum2 ...)
procedure: (fx>= fixnum1 fixnum2 ...)
returns: #t if the relation holds, #f otherwise
libraries: (chezscheme)
The predicate fx= returns #t if its arguments are equal. The predicate fx< returns #t if its arguments are monotonically increasing, i.e., each argument is greater than the preceding ones, while fx> returns #t if its arguments are monotonically decreasing. The predicate fx<= returns #t if its arguments are monotonically nondecreasing, i.e., each argument is not less than the preceding ones, while fx>= returns #t if its arguments are monotonically nonincreasing. When passed only one argument, each of these predicates returns #t.
These procedures are similar to the Revised6 Report procedures fx=?, fx<?, fx>?, fx<=?, and fx>=? except that the Revised6 Report procedures require two or more arguments, and their names have the "?" suffix.
(fx= 0) #t
(fx= 0 0) #t
(fx< (most-negative-fixnum) 0 (most-positive-fixnum)) #t
(let ([x 3]) (fx<= 0 x 9)) #t
(fx<= 0 3 3) #t
(fx>= 0 0 (most-negative-fixnum)) #t
procedure: (fxnonpositive? fixnum)
returns: #t if fixnum is not greater than zero, #f otherwise
procedure: (fxnonnegative? fixnum)
returns: #t if fixnum is not less than zero, #f otherwise
libraries: (chezscheme)
fxnonpositive? is equivalent to (lambda (x) (fx<= x 0)), and fxnonnegative? is equivalent to (lambda (x) (fx>= x 0)).
(fxnonpositive? 128) #f
(fxnonpositive? 0) #t
(fxnonpositive? -1) #t
(fxnonnegative? -65) #f
(fxnonnegative? 0) #t
(fxnonnegative? 1) #t
procedure: (fx+ fixnum ...)
returns: the sum of the arguments fixnum ...
libraries: (chezscheme)
When called with no arguments, fx+ returns 0.
(fx+) 0
(fx+ 1 2) 3
(fx+ 3 4 5) 12
(apply fx+ '(1 2 3 4 5)) 15
procedure: (fx- fixnum1 fixnum2 ...)
returns: a fixnum
libraries: (chezscheme)
When called with one argument, fx- returns the negative of fixnum1. Thus, (fx- fixnum1) is an idiom for (fx- 0 fixnum1).
When called with two or more arguments, fx- returns the result of subtracting the sum of the numbers fixnum2 ... from fixnum1.
(fx- 3) -3
(fx- 4 3) 1
(fx- 4 3 2 1) -2
procedure: (fx* fixnum ...)
returns: the product of the arguments fixnum ...
libraries: (chezscheme)
When called with no arguments, fx* returns 1.
(fx*) 1
(fx* 1 2) 2
(fx* 3 -4 5) -60
(apply fx* '(1 -2 3 -4 5)) 120
procedure: (fx/ fixnum1 fixnum2 ...)
returns: see explanation
libraries: (chezscheme)
When called with one argument, fx/ returns the reciprocal of fixnum1. That is, (fx/ fixnum1) is an idiom for (fx/ 1 fixnum1).
When called with two or more arguments, fx/ returns the result of dividing fixnum1 by the product of the remaining arguments fixnum2 ....
(fx/ 1) 1
(fx/ -17) 0
(fx/ 8 -2) -4
(fx/ -9 2) -4
(fx/ 60 5 3 2) 2
procedure: (fx1+ fixnum)
procedure: (fx1- fixnum)
returns: fixnum plus 1 or fixnum minus 1
libraries: (chezscheme)
(define fxplus
(lambda (x y)
(if (fxzero? x)
y
(fxplus (fx1- x) (fx1+ y)))))
(fxplus 7 8) 15
fx1+ and fx1- can be defined as follows:
(define fx1+ (lambda (x) (fx+ x 1)))
(define fx1- (lambda (x) (fx- x 1)))
procedure: (fxquotient fixnum1 fixnum2 ...)
returns: see explanation
libraries: (chezscheme)
fxquotient is identical to fx/. See the description of fx/ above.
procedure: (fxremainder fixnum1 fixnum2)
returns: the fixnum remainder of fixnum1 divided by fixnum2
libraries: (chezscheme)
The result of fxremainder has the same sign as fixnum1.
(fxremainder 16 4) 0
(fxremainder 5 2) 1
(fxremainder -45 7) -3
(fxremainder 10 -3) 1
(fxremainder -17 -9) -8
procedure: (fxmodulo fixnum1 fixnum2)
returns: the fixnum modulus of fixnum1 and fixnum2
libraries: (chezscheme)
The result of fxmodulo has the same sign as fixnum2.
(fxmodulo 16 4) 0
(fxmodulo 5 2) 1
(fxmodulo -45 7) 4
(fxmodulo 10 -3) -2
(fxmodulo -17 -9) -8
procedure: (fxabs fixnum)
returns: the absolute value of fixnum
libraries: (chezscheme)
(fxabs 1) 1
(fxabs -1) 1
(fxabs 0) 0
Inexact real numbers are normally represented by flonums. A flonum is a single 64-bit double-precision floating point number. This section describes operations on flonums, most of which accept flonum arguments and return flonum values. In most cases, the operations are inline-coded or coded as machine language subroutines at optimize-level 3 with no argument type checking; full type checking is performed at lower optimize levels. Flonum-specific procedure names begin with the prefix "fl" to set them apart from their generic counterparts.
Inexact real numbers may also be represented by inexact complexnums with imaginary parts equal to zero, which cannot be used as input to the flonum-specific operators. Such numbers are produced, however, only from operations involving complex numbers with nonzero imaginary parts, by explicit calls to fl-make-rectangular, make-rectangular, or make-polar, or by numeric input in either polar or rectangular format.
procedure: (flonum->fixnum flonum)
returns: the fixnum representation of flonum, truncated
libraries: (chezscheme)
The truncated value of flonum must fall within the fixnum range. flonum->fixnum is a restricted version of exact, which converts any numeric representation to its exact equivalent.
(flonum->fixnum 0.0) 0
(flonum->fixnum 3.9) 3
(flonum->fixnum -2.2) -2
procedure: (fl= flonum1 flonum2 ...)
procedure: (fl< flonum1 flonum2 ...)
procedure: (fl> flonum1 flonum2 ...)
procedure: (fl<= flonum1 flonum2 ...)
procedure: (fl>= flonum1 flonum2 ...)
returns: #t if the relation holds, #f otherwise
libraries: (chezscheme)
The predicate fl= returns #t if its arguments are equal. The predicate fl< returns #t if its arguments are monotonically increasing, i.e., each argument is greater than the preceding ones, while fl> returns #t if its arguments are monotonically decreasing. The predicate fl<= returns #t if its arguments are monotonically nondecreasing, i.e., each argument is not less than the preceding ones, while fl>= returns #t if its arguments are monotonically nonincreasing. When passed only one argument, each of these predicates returns #t.
IEEE NANs are not comparable, i.e., comparisons involving NANs always return #f.
These procedures are similar to the Revised6 Report procedures fl=?, fl<?, fl>?, fl<=?, and fl>=? except that the Revised6 Report procedures require two or more arguments, and their names have the "?" suffix.
(fl= 0.0) #t
(fl= 0.0 0.0) #t
(fl< -1.0 0.0 1.0) #t
(fl> -1.0 0.0 1.0) #f
(fl<= 0.0 3.0 3.0) #t
(fl>= 4.0 3.0 3.0) #t
(fl< 7.0 +inf.0) #t
(fl= +nan.0 0.0) #f
(fl= +nan.0 +nan.0) #f
(fl< +nan.0 +nan.0) #f
(fl> +nan.0 +nan.0) #f
procedure: (flnonpositive? fl)
returns: #t if fl is not greater than zero, #f otherwise
procedure: (flnonnegative? fl)
returns: #t if fl is not less than zero, #f otherwise
libraries: (chezscheme)
flnonpositive? is equivalent to (lambda (x) (fl<= x 0.0)), and flnonnegative? is equivalent to (lambda (x) (fl>= x 0.0)).
Even if the flonum representation distinguishes -0.0 from +0.0, both are considered nonpositive and nonnegative.
(flnonpositive? 128.0) #f
(flnonpositive? 0.0) #t
(flnonpositive? -0.0) #t
(flnonpositive? -1.0) #t
(flnonnegative? -65.0) #f
(flnonnegative? 0.0) #t
(flnonnegative? -0.0) #t
(flnonnegative? 1.0) #t
(flnonnegative? +nan.0) #f
(flnonpositive? +nan.0) #f
(flnonnegative? +inf.0) #t
(flnonnegative? -inf.0) #f
procedure: (decode-float x)
returns: see below
libraries: (chezscheme)
x must be a flonum. decode-float returns a vector with three integer elements, m, e, and s, such that x = sm2e. It is useful primarily in the printing of floating-point numbers.
(decode-float 1.0) #(4503599627370496 -52 1)
(decode-float -1.0) #(4503599627370496 -52 -1)
(define slow-identity
(lambda (x)
(inexact
(let ([v (decode-float x)])
(let ([m (vector-ref v 0)]
[e (vector-ref v 1)]
[s (vector-ref v 2)])
(* s m (expt 2 e)))))))
(slow-identity 1.0) 1.0
(slow-identity -1e20) -1e20
procedure: (fllp flonum)
returns: see below
libraries: (chezscheme)
fllp returns the 12-bit integer consisting of the exponent plus highest order represented bit of a flonum (ieee 64-bit floating-point number). It can be used to compute a fast approximation of the logarithm of the number.
(fllp 0.0) 0
(fllp 1.0) 2046
(fllp -1.0) 2046
(fllp 1.5) 2047
(fllp +inf.0) 4094
(fllp -inf.0) 4094
(fllp #b1.0e-1111111111) 1
(fllp #b1.0e-10000000000) 0
The procedures described in this section provide mechanisms for creating and operating on inexact complex numbers. Inexact complex numbers with nonzero imaginary parts are represented as inexact complexnums. An inexact complexnum contains two 64-bit double-precision floating point numbers. Inexact complex numbers with imaginary parts equal to zero (in other words, inexact real numbers) may be represented as either inexact complexnums or flonums. The operations described in this section accept any mix of inexact complexnum and flonum arguments (collectively, "cflonums").
In most cases, the operations are performed with minimal type checking at optimize-level 3; full type checking is performed at lower optimize levels. Inexact complex procedure names begin with the prefix "cfl" to set them apart from their generic counterparts.
procedure: (fl-make-rectangular flonum1 flonum2)
returns: an inexact complexnum
libraries: (chezscheme)
The inexact complexnum produced by fl-make-rectangular has real part equal to flonum1 and imaginary part equal to flonum2.
(fl-make-rectangular 2.0 -3.0) 2.0-3.0i
(fl-make-rectangular 2.0 0.0) 2.0+0.0i
(fl-make-rectangular 2.0 -0.0) 2.0-0.0i
procedure: (cfl-real-part cflonum)
returns: the real part of cflonum
procedure: (cfl-imag-part cflonum)
returns: the imaginary part of cflonum
libraries: (chezscheme)
(cfl-real-part 2.0-3.0i) 2.0
(cfl-imag-part 2.0-3.0i) -3.0
(cfl-imag-part 2.0-0.0i) -0.0
(cfl-imag-part 2.0-inf.0i) -inf.0
procedure: (cfl= cflonum ...)
returns: #t if its arguments are equal, #f otherwise
libraries: (chezscheme)
(cfl= 7.0+0.0i 7.0) #t
(cfl= 1.0+2.0i 1.0+2.0i) #t
(cfl= 1.0+2.0i 1.0-2.0i) #f
procedure: (cfl+ cflonum ...)
procedure: (cfl* cflonum ...)
procedure: (cfl- cflonum1 cflonum2 ...)
procedure: (cfl/ cflonum1 cflonum2 ...)
returns: a cflonum
libraries: (chezscheme)
These procedures compute the sum, difference, product, or quotient of inexact complex quantities, whether these quantities are represented by flonums or inexact complexnums. For example, if cfl+ receives two flonum arguments a and b, it returns the sum a + b; in this case, it behaves the same as fl+. With two inexact complexnum arguments a + bi and c + di, it returns the sum (a + c) + (b + d)i. If one argument is a flonum a and the other an inexact complexnum c + di, cfl+ returns (a + c) + di.
When passed zero arguments, cfl+ returns 0.0 and cfl* returns 1.0. When passed one argument, cfl- returns the additive inverse of the argument, and cfl/ returns the multiplicative inverse of the argument. When passed three or more arguments, cfl- returns the difference between its first and the sum of its remaining arguments, and cfl/ returns the quotient of its first and the product of its remaining arguments.
(cfl+) 0.0
(cfl*) 1.0
(cfl- 5.0+1.0i) -5.0-1.0i
(cfl/ 2.0+2.0i) 0.25-0.25i
(cfl+ 1.0+2.2i -3.7+5.3i) -2.7+7.5i
(cfl+ 1.0 -5.3) -4.3
(cfl+ 1.0 2.0 -5.3i) 3.0-5.3i
(cfl- 1.0+2.5i -3.7) 4.7+2.5i
(cfl* 1.0+2.0i 3.0+4.0i) -5.0+10.0i
(cfl/ -5.0+10.0i 1.0+2.0i 2.0) 1.5+2.0i
procedure: (cfl-conjugate cflonum)
returns: complex conjugate of cflonum
libraries: (chezscheme)
The procedure cfl-conjugate, when passed an inexact complex argument a + bi, returns its complex conjugate a + (-b)i.
See also conjugate, which is a generic version of this operator that returns the complex conjugate of any valid representation for a complex number.
(cfl-conjugate 3.0) 3.0
(cfl-conjugate 3.0+4.0i) 3.0-4.0i
(cfl-conjugate 1e-20-2e-30i) 1e-20+2e-30i
procedure: (cfl-magnitude-squared cflonum)
returns: magnitude of cflonum squared
libraries: (chezscheme)
The procedure cfl-magnitude-squared, when passed an inexact complex argument a + bi returns a flonum representing the magnitude of the argument squared, i.e., a2 + b2.
See also magnitude-squared, which is a generic version of this operator that returns the magnitude squared of any valid representation for a complex number. Both operations are similar to the magnitude procedure, which returns the magnitude, sqrt(a2 + b2), of its generic complex argument.
(cfl-magnitude-squared 3.0) 9.0
(cfl-magnitude-squared 3.0-4.0i) 25.0
Chez Scheme provides a set of logical operators that allow exact integers (fixnums and bignums) to be treated as sets or sequences of bits. These operators include logand (bitwise logical and), logior (bitwise logical or), logxor (bitwise logical exclusive or), lognot (bitwise logical not), logtest (test multiple bits), logbit? (test single bit), logbit0 (reset single bit), logbit1 (set single bit), and ash (arithmetic shift). Each of these operators treats its arguments as two's complement integers, regardless of the underlying representation. This treatment can be exploited to represent infinite sets: a negative number represents an infinite number of one bits beyond the leftmost zero, and a nonnegative number represents an infinite number of zero bits beyond the leftmost one bit.
Fixnum equivalents of the logical operators are provided, as fxlogand, fxlogior, fxlogxor, fxlognot, fxlogtest, fxlogbit?, fxlogbit0, and fxlogbit1. Three separate fixnum operators are provided for shifting: fxsll (shift-left logical), fxsrl (shift-right logical), fxsra (shift-right arithmetic). Logical and arithmetic shifts differ only for right shifts. Shift-right logical shifts in zero bits on the left end, and shift-right arithmetic replicates the sign bit.
Logical shifts do not make sense for arbitrary-precision integers, since these have no "left end" into which bits must be shifted.
procedure: (logand int ...)
returns: the logical "and" of the arguments int ...
libraries: (chezscheme)
The arguments must be exact integers (fixnums or bignums) and are treated as two's complement integers, regardless of the underlying representation. With no arguments, logand returns -1, i.e., all bits set.
(logand) -1
(logand 15) 15
(logand -1 -1) -1
(logand -1 0) 0
(logand 5 3) 1
(logand #x173C8D95 7) 5
(logand #x173C8D95 -8) #x173C8D90
(logand #b1100 #b1111 #b1101) #b1100
procedure: (logior int ...)
procedure: (logor int ...)
returns: the logical "or" of the arguments int ...
libraries: (chezscheme)
The arguments must be exact integers (fixnums or bignums) and are treated as two's complement integers, regardless of the underlying representation. With no arguments, logior returns 0, i.e., all bits reset.
(logior) 0
(logior 15) 15
(logior -1 -1) -1
(logior -1 0) -1
(logior 5 3) 7
(logior #b111000 #b101010) #b111010
(logior #b1000 #b0100 #b0010) #b1110
(apply logior '(1 2 4 8 16)) 31
procedure: (logxor int ...)
returns: the logical "exclusive or" of the arguments int ...
libraries: (chezscheme)
The arguments must be exact integers (fixnums or bignums) and are treated as two's complement integers, regardless of the underlying representation. With no arguments, logxor returns 0, i.e., all bits reset.
(logxor) 0
(logxor 15) 15
(logxor -1 -1) 0
(logxor -1 0) -1
(logxor 5 3) 6
(logxor #b111000 #b101010) #b010010
(logxor #b1100 #b0100 #b0110) #b1110
procedure: (lognot int)
returns: the logical "not" of int
libraries: (chezscheme)
The argument must be an exact integer (fixnum or bignum) and is treated as a two's complement integer, regardless of the underlying representation.
(lognot -1) 0
(lognot 0) -1
(lognot 7) -8
(lognot -8) 7
procedure: (logbit? index int)
returns: #t if the specified bit is set, otherwise #f
libraries: (chezscheme)
index must be a nonnegative exact integer. int must be an exact integer (fixnum or bignum) and is treated as a two's complement integer, regardless of the underlying representation.
logbit? returns #t if the bit at index index of int is set (one) and #f otherwise. The index is zero-based, counting from the lowest-order toward higher-order bits. There is no upper limit on the index; for nonnegative values of int, the bits above the highest order set bit are all considered to be zero, and for negative values, the bits above the highest order reset bit are all considered to be one.
logbit? is equivalent to
(lambda (k n) (not (zero? (logand n (ash 1 k)))))
but more efficient.
(logbit? 0 #b1110) #f
(logbit? 1 #b1110) #t
(logbit? 2 #b1110) #t
(logbit? 3 #b1110) #t
(logbit? 4 #b1110) #f
(logbit? 100 #b1110) #f
(logbit? 0 -6) #f ; the two's complement of -6 is 1...1010
(logbit? 1 -6) #t
(logbit? 2 -6) #f
(logbit? 3 -6) #t
(logbit? 100 -6) #t
(logbit? (random 1000000) 0) #f
(logbit? (random 1000000) -1) #t
(logbit? 20000 (ash 1 20000)) #t
procedure: (logtest int1 int2)
returns: #t if any common bits are set, otherwise #f
libraries: (chezscheme)
The arguments must be exact integers (fixnums or bignums) and are treated as two's complement integers, regardless of the underlying representation.
logtest returns #t if any bit set in one argument is also set in the other. It returns #f if the two arguments have no set bits in common.
logtest is equivalent to
(lambda (n1 n2) (not (zero? (logand n1 n2))))
but more efficient.
(logtest #b10001 #b1110) #f
(logtest #b10101 #b1110) #t
(logtest #b111000 #b110111) #t
(logtest #b101 -6) #f ; the two's complement of -6 is 1...1010
(logtest #b1000 -6) #t
(logtest 100 -6) #t
(logtest (+ (random 1000000) 1) 0) #f
(logtest (+ (random 1000000) 1) -1) #t
(logtest (ash #b101 20000) (ash #b111 20000)) #t
procedure: (logbit0 index int)
returns: the result of clearing bit index of int
libraries: (chezscheme)
index must be a nonnegative exact integer. int must be an exact integer (fixnum or bignum) and is treated as a two's complement integer, regardless of the underlying representation.
The index is zero-based, counting from the lowest-order toward higher-order bits. As with logbit?, there is no upper limit on the index.
logbit0 is equivalent to
(lambda (i n) (logand (lognot (ash 1 i)) n))
but more efficient.
(logbit0 3 #b10101010) #b10100010
(logbit0 4 #b10101010) #b10101010
(logbit0 0 -1) -2
procedure: (logbit1 index int)
returns: the result of setting bit index of int
libraries: (chezscheme)
index must be a nonnegative exact integer. int must be an exact integer (fixnum or bignum) and is treated as a two's complement integer, regardless of the underlying representation.
The index is zero-based, counting from the lowest-order toward higher-order bits. As with logbit?, there is no upper limit on the index.
logbit1 is equivalent to
(lambda (i n) (logor (ash 1 i) n))
but more efficient.
(logbit1 3 #b10101010) #b10101010
(logbit1 4 #b10101010) #b10111010
(logbit1 4 0) #b10000
(logbit1 0 -2) -1
procedure: (ash int count)
returns: int shifted left arithmetically by count.
libraries: (chezscheme)
Both arguments must be exact integers. The first argument is treated as a two's complement integer, regardless of the underlying representation. If count is negative, int is shifted right by -count bits.
(ash 8 0) 8
(ash 8 2) 32
(ash 8 -2) 2
(ash -1 2) -4
(ash -1 -2) -1
procedure: (fxlogand fixnum ...)
returns: the logical "and" of the arguments fixnum ...
libraries: (chezscheme)
The arguments are treated as two's complement integers, regardless of the underlying representation. With no arguments, fxlogand returns -1, i.e., all bits set.
(fxlogand) -1
(fxlogand 15) 15
(fxlogand -1 -1) -1
(fxlogand -1 0) 0
(fxlogand 5 3) 1
(fxlogand #b111000 #b101010) #b101000
(fxlogand #b1100 #b1111 #b1101) #b1100
procedure: (fxlogior fixnum ...)
procedure: (fxlogor fixnum ...)
returns: the logical "or" of the arguments fixnum ...
libraries: (chezscheme)
The arguments are treated as two's complement integers, regardless of the underlying representation. With no arguments, fxlogior returns 0, i.e., all bits reset.
(fxlogior) 0
(fxlogior 15) 15
(fxlogior -1 -1) -1
(fxlogior -1 0) -1
(fxlogior #b111000 #b101010) #b111010
(fxlogior #b1000 #b0100 #b0010) #b1110
(apply fxlogior '(1 2 4 8 16)) 31
procedure: (fxlogxor fixnum ...)
returns: the logical "exclusive or" of the arguments fixnum ...
libraries: (chezscheme)
The arguments are treated as two's complement integers, regardless of the underlying representation. With no arguments, fxlogxor returns 0, i.e., all bits reset.
(fxlogxor) 0
(fxlogxor 15) 15
(fxlogxor -1 -1) 0
(fxlogxor -1 0) -1
(fxlogxor 5 3) 6
(fxlogxor #b111000 #b101010) #b010010
(fxlogxor #b1100 #b0100 #b0110) #b1110
procedure: (fxlognot fixnum)
returns: the logical "not" of fixnum
libraries: (chezscheme)
The argument is treated as a two's complement integer, regardless of the underlying representation.
(fxlognot -1) 0
(fxlognot 0) -1
(fxlognot 1) -2
(fxlognot -2) 1
procedure: (fxlogbit? index fixnum)
returns: #t if the specified bit is set, otherwise #f
libraries: (chezscheme)
index must be a nonnegative fixnum. fixnum is treated as a two's complement integer, regardless of the underlying representation.
fxlogbit? returns #t if the bit at index index of fixnum is set (one) and #f otherwise. The index is zero-based, counting from the lowest-order toward higher-order bits. The index is limited only by the fixnum range; for nonnegative values of fixnum, the bits above the highest order set bit are all considered to be zero, and for negative values, the bits above the highest order reset bit are all considered to be one.
(fxlogbit? 0 #b1110) #f
(fxlogbit? 1 #b1110) #t
(fxlogbit? 2 #b1110) #t
(fxlogbit? 3 #b1110) #t
(fxlogbit? 4 #b1110) #f
(fxlogbit? 100 #b1110) #f
(fxlogbit? 0 -6) #f ; the two's complement of -6 is 1...1010
(fxlogbit? 1 -6) #t
(fxlogbit? 2 -6) #f
(fxlogbit? 3 -6) #t
(fxlogbit? 100 -6) #t
(fxlogbit? (random 1000000) 0) #f
(fxlogbit? (random 1000000) -1) #t
procedure: (fxlogtest fixnum1 fixnum2)
returns: #t if any common bits are set, otherwise #f
libraries: (chezscheme)
The arguments are treated as two's complement integers, regardless of the underlying representation.
fxlogtest returns #t if any bit set in one argument is also set in the other. It returns #f if the two arguments have no set bits in common.
(fxlogtest #b10001 #b1110) #f
(fxlogtest #b10101 #b1110) #t
(fxlogtest #b111000 #b110111) #t
(fxlogtest #b101 -6) #f ; the two's complement of -6 is 1...1010
(fxlogtest #b1000 -6) #t
(fxlogtest 100 -6) #t
(fxlogtest (+ (random 1000000) 1) 0) #f
(fxlogtest (+ (random 1000000) 1) -1) #t
procedure: (fxlogbit0 index fixnum)
returns: the result of clearing bit index of fixnum
libraries: (chezscheme)
fixnum is treated as a two's complement integer, regardless of the underlying representation. index must be nonnegative and less than the number of bits in a fixnum, excluding the sign bit, i.e., less than (integer-length (most-positive-fixnum)). The index is zero-based, counting from the lowest-order toward higher-order bits.
fxlogbit0 is equivalent to
(lambda (i n) (fxlogand (fxlognot (fxsll 1 i)) n))
but more efficient.
(fxlogbit0 3 #b10101010) #b10100010
(fxlogbit0 4 #b10101010) #b10101010
(fxlogbit0 0 -1) -2
procedure: (fxlogbit1 index fixnum)
returns: the result of setting bit index of fixnum
libraries: (chezscheme)
fixnum is treated as a two's complement integer, regardless of the underlying representation. index must be nonnegative and less than the number of bits in a fixnum, excluding the sign bit, i.e., less than (integer-length (most-positive-fixnum)). The index is zero-based, counting from the lowest-order toward higher-order bits.
fxlogbit1 is equivalent to
(lambda (i n) (fxlogor (fxsll 1 i) n))
but more efficient.
(fxlogbit1 3 #b10101010) #b10101010
(fxlogbit1 4 #b10101010) #b10111010
(fxlogbit1 4 0) #b10000
(fxlogbit1 0 -2) -1
procedure: (fxsll fixnum count)
returns: fixnum shifted left by count
libraries: (chezscheme)
fixnum is treated as a two's complement integer, regardless of the underlying representation. count must be nonnegative and not more than the number of bits in a fixnum, i.e., (+ (integer-length (most-positive-fixnum)) 1). An exception is raised with condition-type &implementation-restriction if the result cannot be represented as a fixnum.
(fxsll 1 2) 4
(fxsll -1 2) -4
procedure: (fxsrl fixnum count)
returns: fixnum logically shifted right by count
libraries: (chezscheme)
fixnum is treated as a two's complement integer, regardless of the underlying representation. count must be nonnegative and not more than the number of bits in a fixnum, i.e., (+ (integer-length (most-positive-fixnum)) 1).
(fxsrl 4 2) 1
(= (fxsrl -1 1) (most-positive-fixnum)) #t
procedure: (fxsra fixnum count)
returns: fixnum arithmetically shifted right by count
libraries: (chezscheme)
fixnum is treated as a two's complement integer, regardless of the underlying representation. count must be nonnegative and not more than the number of bits in a fixnum, i.e., (+ (integer-length (most-positive-fixnum)) 1).
(fxsra 64 3) 8
(fxsra -1 1) -1
(fxsra -64 3) -8
procedure: (random real)
returns: a nonnegative pseudo-random number less than real
libraries: (chezscheme)
real must be a positive integer or positive inexact real number.
(random 1) 0
(random 1029384535235) 1029384535001, every now and then
(random 1.0) 0.5, every now and then
thread parameter: random-seed
libraries: (chezscheme)
The random number generator allows the current random seed to be obtained and modified via the parameter random-seed.
When called without arguments, random-seed returns the current random seed. When called with one argument, which must be a nonnegative exact integer ranging from 1 through 232 - 1, random-seed sets the current random seed to the argument.
(let ([s (random-seed)])
(let ([r1 (random 1.0)])
(random-seed s)
(eqv? (random 1.0) r1))) #t
procedure: (= num1 num2 num3 ...)
procedure: (< real1 real2 real3 ...)
procedure: (> real1 real2 real3 ...)
procedure: (<= real1 real2 real3 ...)
procedure: (>= real1 real2 real3 ...)
returns: #t if the relation holds, #f otherwise
libraries: (chezscheme)
These predicates are identical to the Revised6 Report counterparts, except they are extended to accept one or more rather than two or more arguments. When passed one argument, each of these predicates returns #t.
(> 3/4) #t
(< 3/4) #t
(= 3/4) #t
procedure: (1+ num)
procedure: (add1 num)
procedure: (1- num)
procedure: (-1+ num)
procedure: (sub1 num)
returns: num plus 1 or num minus 1
libraries: (chezscheme)
1+ and add1 are equivalent to (lambda (x) (+ x 1)); 1-, -1+, and sub1 are equivalent to (lambda (x) (- x 1)).
(define plus
; x should be a nonnegative integer
(lambda (x y)
(if (zero? x)
y
(plus (1- x) (1+ y)))))
(plus 7 8) 15
(define double
; x should be a nonnegative integer
(lambda (x)
(if (zero? x)
0
(add1 (add1 (double (sub1 x)))))))
(double 7) 14
procedure: (expt-mod int1 int2 int3)
returns: int1 raised to the int2 power, modulo int3
libraries: (chezscheme)
int1, int2 and int3 must be nonnegative integers. expt-mod performs its computation in such a way that the intermediate results are never much larger than int3. This means that when int2 is large, expt-mod is more efficient than the equivalent procedure (lambda (x y z) (modulo (expt x y) z)).
(expt-mod 2 4 3) 1
(expt-mod 2 76543 76543) 2
procedure: (isqrt n)
returns: the integer square root of n
libraries: (chezscheme)
n must be a nonnegative integer.
The integer square root of n is defined to be
.
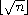(isqrt 0) 0
(isqrt 16) 4
(isqrt 16.0) 4.0
(isqrt 20) 4
(isqrt 20.0) 4.0
(isqrt (* 2 (expt 10 20))) 14142135623
procedure: (integer-length n)
returns: see below
libraries: (chezscheme)
The procedure integer-length returns the length in bits of the smallest two's complement representation for n, with an assumed leading 1 (sign) bit for negative numbers. For zero, integer-length returns 0.
(integer-length 0) 0
(integer-length 1) 1
(integer-length 2) 2
(integer-length 3) 2
(integer-length 4) 3
(integer-length #b10000000) 8
(integer-length #b11111111) 8
(integer-length -1) 0
(integer-length -2) 1
(integer-length -3) 2
(integer-length -4) 2
procedure: (nonpositive? real)
returns: #t if real is not greater than zero, #f otherwise
libraries: (chezscheme)
nonpositive? is equivalent to (lambda (x) (<= x 0)).
(nonpositive? 128) #f
(nonpositive? 0.0) #t
(nonpositive? 1.8e-15) #f
(nonpositive? -2/3) #t
procedure: (nonnegative? real)
returns: #t if real is not less than zero, #f otherwise
libraries: (chezscheme)
nonnegative? is equivalent to (lambda (x) (>= x 0)).
(nonnegative? -65) #f
(nonnegative? 0) #t
(nonnegative? -0.0121) #f
(nonnegative? 15/16) #t
procedure: (conjugate num)
returns: complex conjugate of num
libraries: (chezscheme)
The procedure conjugate, when passed a complex argument a + bi, returns its complex conjugate a + (-b)i.
(conjugate 3.0+4.0i) 3.0-4.0i
(conjugate 1e-20-2e-30i) 1e-20+2e-30i
(conjugate 3) 3
procedure: (magnitude-squared num)
returns: magnitude of num squared
libraries: (chezscheme)
The procedure magnitude-squared, when passed a complex argument a + bi returns its magnitude squared, i.e., a2 + b2.
(magnitude-squared 3.0-4.0i) 25.0
(magnitude-squared 3.0) 9.0
procedure: (sinh num)
procedure: (cosh num)
procedure: (tanh num)
returns: the hyperbolic sine, cosine, or tangent of num
libraries: (chezscheme)
(sinh 0.0) 0.0
(cosh 0.0) 1.0
(tanh -0.0) -0.0
procedure: (asinh num)
procedure: (acosh num)
procedure: (atanh num)
returns: the hyperbolic arc sine, arc cosine, or arc tangent of num
libraries: (chezscheme)
(acosh 0.0) 0.0+1.5707963267948966i
(acosh 1.0) 0.0
(atanh -1.0) -inf.0
procedure: (string->number string)
procedure: (string->number string radix)
returns: the number represented by string, or #f
libraries: (chezscheme)
This procedure is identical to the Revised6 Report version except that radix may be any exact integer between 2 and 36, inclusive. The Revised6 Report version requires radix to be in the set {2,8,10,16}.
(string->number "211012" 3) 559
(string->number "tobeornottobe" 36) 140613689159812836698
procedure: (number->string num)
procedure: (number->string num radix)
procedure: (number->string num radix precision)
returns: an external representation of num as a string
libraries: (chezscheme)
This procedure is identical to the Revised6 Report version except that radix may be any exact integer between 2 and 36, inclusive. The Revised6 Report version requires radix to be in the set {2,8,10,16}.
(number->string 10000 4) "2130100"
(number->string 10000 27) "DJA"
Chez Scheme Version 9 User's Guide
Copyright © 2023 Cisco Systems, Inc.
Licensed under the Apache License Version 2.0
(full copyright notice.).
Revised October 2023 for Chez Scheme Version 9.6.4
about this book